Rectified 8-simplexes
 8-simplex |
 Rectified 8-simplex | ||
 Birectified 8-simplex |
 Trirectified 8-simplex | ||
| Orthogonal projections in A8 Coxeter plane | |||
|---|---|---|---|
In eight-dimensional geometry, a rectified 8-simplex is a convex uniform 8-polytope, being a rectification of the regular 8-simplex.
There are unique 3 degrees of rectifications in regular 8-polytopes. Vertices of the rectified 8-simplex are located at the edge-centers of the 8-simplex. Vertices of the birectified 8-simplex are located in the triangular face centers of the 8-simplex. Vertices of the trirectified 8-simplex are located in the tetrahedral cell centers of the 8-simplex.
Rectified 8-simplex
| Rectified 8-simplex | |
|---|---|
| Type | uniform 8-polytope |
| Coxeter symbol | 061 |
| Schläfli symbol | t1{37} r{37} = {36,1} or |
| Coxeter-Dynkin diagrams | or |
| 7-faces | 18 |
| 6-faces | 108 |
| 5-faces | 336 |
| 4-faces | 630 |
| Cells | 756 |
| Faces | 588 |
| Edges | 252 |
| Vertices | 36 |
| Vertex figure | 7-simplex prism, {}×{3,3,3,3,3} |
| Petrie polygon | enneagon |
| Coxeter group | A8, [37], order 362880 |
| Properties | convex |
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as S1
8. It is also called 06,1 for its branching Coxeter-Dynkin diagram, shown as ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Coordinates
The Cartesian coordinates of the vertices of the rectified 8-simplex can be most simply positioned in 9-space as permutations of (0,0,0,0,0,0,0,1,1). This construction is based on facets of the rectified 9-orthoplex.
Images
| Ak Coxeter plane | A8 | A7 | A6 | A5 |
|---|---|---|---|---|
| Graph |  |
 |
 |
 |
| Dihedral symmetry | [9] | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 | |
| Graph |  |
 |
 | |
| Dihedral symmetry | [5] | [4] | [3] |
Birectified 8-simplex
| Birectified 8-simplex | |
|---|---|
| Type | uniform 8-polytope |
| Coxeter symbol | 052 |
| Schläfli symbol | t2{37} 2r{37} = {35,2} or |
| Coxeter-Dynkin diagrams | or |
| 7-faces | 18 |
| 6-faces | 144 |
| 5-faces | 588 |
| 4-faces | 1386 |
| Cells | 2016 |
| Faces | 1764 |
| Edges | 756 |
| Vertices | 84 |
| Vertex figure | {3}×{3,3,3,3} |
| Coxeter group | A8, [37], order 362880 |
| Properties | convex |
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as S2
8. It is also called 05,2 for its branching Coxeter-Dynkin diagram, shown as ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The birectified 8-simplex is the vertex figure of the 152 honeycomb.
Coordinates
The Cartesian coordinates of the vertices of the birectified 8-simplex can be most simply positioned in 9-space as permutations of (0,0,0,0,0,0,1,1,1). This construction is based on facets of the birectified 9-orthoplex.
Images
| Ak Coxeter plane | A8 | A7 | A6 | A5 |
|---|---|---|---|---|
| Graph |  |
 |
 |
 |
| Dihedral symmetry | [9] | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 | |
| Graph |  |
 |
 | |
| Dihedral symmetry | [5] | [4] | [3] |
Trirectified 8-simplex
| Trirectified 8-simplex | |
|---|---|
| Type | uniform 8-polytope |
| Coxeter symbol | 043 |
| Schläfli symbol | t3{37} 3r{37} = {34,3} or |
| Coxeter-Dynkin diagrams | or |
| 7-faces | 18 |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 1260 |
| Vertices | 126 |
| Vertex figure | {3,3}×{3,3,3} |
| Petrie polygon | enneagon |
| Coxeter group | A7, [37], order 362880 |
| Properties | convex |
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as S3
8. It is also called 04,3 for its branching Coxeter-Dynkin diagram, shown as ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Coordinates
The Cartesian coordinates of the vertices of the trirectified 8-simplex can be most simply positioned in 9-space as permutations of (0,0,0,0,0,1,1,1,1). This construction is based on facets of the trirectified 9-orthoplex.
Images
| Ak Coxeter plane | A8 | A7 | A6 | A5 |
|---|---|---|---|---|
| Graph |  |
 |
 |
 |
| Dihedral symmetry | [9] | [8] | [7] | [6] |
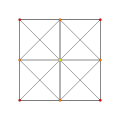
| Ak Coxeter plane | A4 | A3 | A2 | |
| Graph | 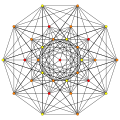 |
 |
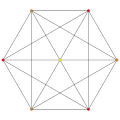 | |
| Dihedral symmetry | [5] | [4] | [3] |
Related polytopes
This polytope is the vertex figure of the 9-demicube, and the edge figure of the uniform 261 honeycomb.
It is also one of 135 uniform 8-polytopes with A8 symmetry.
| A8 polytopes | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
t0 |
t1 |
t2 |
t3 |
t01 |
t02 |
t12 |
t03 |
t13 |
t23 |
t04 |
t14 |
t24 |
t34 |
t05 |
t15 |
t25 |
t06 |
t16 |
t07 |
t012 |
t013 |
t023 |
t123 |
t014 |
t024 |
t124 |
t034 |
t134 |
t234 |
t015 |
t025 |
t125 |
t035 |
t135 |
t235 |
t045 |
t145 |
t016 |
t026 |
t126 |
t036 |
t136 |
t046 |
t056 |
t017 |
t027 |
t037 |
t0123 |
t0124 |
t0134 |
t0234 |
t1234 |
t0125 |
t0135 |
t0235 |
t1235 |
t0145 |
t0245 |
t1245 |
t0345 |
t1345 |
t2345 |
t0126 |
t0136 |
t0236 |
t1236 |
t0146 |
t0246 |
t1246 |
t0346 |
t1346 |
t0156 |
t0256 |
t1256 |
t0356 |
t0456 |
t0127 |
t0137 |
t0237 |
t0147 |
t0247 |
t0347 |
t0157 |
t0257 |
t0167 |
t01234 |
t01235 |
t01245 |
t01345 |
t02345 |
t12345 |
t01236 |
t01246 |
t01346 |
t02346 |
t12346 |
t01256 |
t01356 |
t02356 |
t12356 |
t01456 |
t02456 |
t03456 |
t01237 |
t01247 |
t01347 |
t02347 |
t01257 |
t01357 |
t02357 |
t01457 |
t01267 |
t01367 |
t012345 |
t012346 |
t012356 |
t012456 |
t013456 |
t023456 |
t123456 |
t012347 |
t012357 |
t012457 |
t013457 |
t023457 |
t012367 |
t012467 |
t013467 |
t012567 |
t0123456 |
t0123457 |
t0123467 |
t0123567 |
t01234567 |
Notes
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "8D Uniform polytopes (polyzetta)". o3x3o3o3o3o3o3o - rene, o3o3x3o3o3o3o3o - brene, o3o3o3x3o3o3o3o - trene
External links
- Olshevsky, George. "Simplex". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||