q-Weibull distribution

q-Weibull distribution
Probability density function
Cumulative distribution function
Parameters	$q<2$ shape (real) $\lambda >0$ rate (real) $\kappa >0\,$ shape (real)
Support	$x\in [0;+\infty )\!{\text{ for }}q\geq 1$ $x\in [0;{\lambda \over {(1-q)^{1/\kappa }}}){\text{ for }}q<1$
PDF	${\begin{cases}(2-q){\frac {\kappa }{\lambda }}\left({\frac {x}{\lambda }}\right)^{\kappa -1}e_{q}^{-(x/\lambda )^{\kappa }}&x\geq 0\\0&x<0\end{cases}}$
CDF	${\begin{cases}1-e_{q'}^{-(x/\lambda ')^{\kappa }}&x\geq 0\\0&x<0\end{cases}}$
Mean	(see article)

In statistics, the q-Weibull distribution is a probability distribution that generalizes the Weibull distribution and the Lomax distribution (Pareto Type II). It is one example of a Tsallis distribution.

Characterization

Probability density function

The probability density function of a q-Weibull random variable is:^[1]

f(x;q,\lambda ,\kappa )={\begin{cases}(2-q){\frac {\kappa }{\lambda }}\left({\frac {x}{\lambda }}\right)^{\kappa -1}e_{q}(-(x/\lambda )^{\kappa })&x\geq 0,\\0&x<0,\end{cases}}

where q < 2, $\kappa$ > 0 are shape parameters and λ > 0 is the scale parameter of the distribution and

e_q(x) = \begin{cases} \exp(x) & \text{if }q=1, \\[6pt] [1+(1-q)x]^{1/(1-q)} & \text{if }q \ne 1 \text{ and } 1+(1-q)x >0, \\[6pt] 0^{1/(1-q)} & \text{if }q \ne 1\text{ and }1+(1-q)x \le 0, \\[6pt] \end{cases}

is the q-exponential^[1]^[2]^[3]

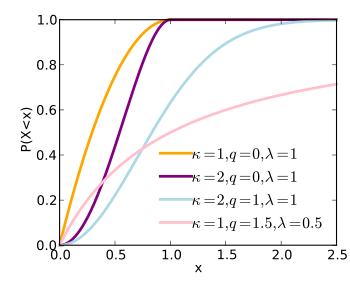
Cumulative distribution function

The cumulative distribution function of a q-Weibull random variable is:

{\begin{cases}1-e_{q'}^{-(x/\lambda ')^{\kappa }}&x\geq 0\\0&x<0\end{cases}}

where

\lambda '={\lambda  \over (2-q)^{1 \over \kappa }}

q'={1 \over (2-q)}

Mean

The mean of the q-Weibull distribution is

\mu (q,\kappa ,\lambda )={\begin{cases}\lambda \,\left(2+{\frac {1}{1-q}}+{\frac {1}{\kappa }}\right)(1-q)^{-{\frac {1}{\kappa }}}\,B\left[1+{\frac {1}{\kappa }},2+{\frac {1}{1-q}}\right]&q<1\\\lambda \,\Gamma (1+{\frac {1}{\kappa }})&q=1\\\lambda \,(2-q)(q-1)^{-{\frac {1+\kappa }{\kappa }}}\,B\left[1+{\frac {1}{\kappa }},-\left(1+{\frac {1}{q-1}}+{\frac {1}{\kappa }}\right)\right]&1<q<1+{\frac {1+2\kappa }{1+\kappa }}\\\infty &1+{\frac {\kappa }{\kappa +1}}\leq q<2\end{cases}}

where $B()$ is the Beta function and $\Gamma ()$ is the Gamma function. The expression for the mean is a continuous function of q over the range of definition for which it is finite.

Relationship to other distributions

The q-Weibull is equivalent to the Weibull distribution when q = 1 and equivalent to the q-exponential when $\kappa =1$

The q-Weibull is a generalization of the Weibull, as it extends this distribution to the cases of finite support (q < 1) and to include heavy-tailed distributions $(q\geq 1+{\frac {\kappa }{\kappa +1}})$ .

The q-Weibull is a generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support and adds the $\kappa$ parameter. The Lomax parameters are:

\alpha ={{2-q} \over {q-1}}~,~\lambda _{\text{Lomax}}={1 \over {\lambda (q-1)}}

As the Lomax distribution is a shifted version of the Pareto distribution, the q-Weibull for $\kappa =1$ is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically:

{\text{If }}X\sim {\text{q-Weibull}}(q,\lambda ,\kappa =1){\text{ and }}Y\sim \left[{\text{Pareto}}\left(x_{m}={1 \over {\lambda (q-1)}},\alpha ={{2-q} \over {q-1}}\right)-x_{m}\right],{\text{ then }}X\sim Y\,

References

1 2 Picoli, S. Jr.; Mendes, R. S.; Malacarne, L. C. (2003). "q-exponential, Weibull, and q-Weibull distributions: an empirical analysis". arXiv:cond-mat/0301552.
↑ Naudts, Jan (2010). "The q-exponential family in statistical physics" (PDF). J. Phys. Conf. Ser. IOP Publishing. 201. doi:10.1088/1742-6596/201/1/012003. Retrieved 9 June 2014.
↑ "On a q-Central Limit Theorem Consistent with Nonextensive Statistical Mechanics" (PDF). Milan J. Math. 76. 2008. doi:10.1007/s00032-008-0087-y. Retrieved 9 June 2014.

Tsallis statistics

Constantino Tsallis Tsallis entropy Tsallis statistics Tsallis distribution q-Gaussian distribution q-exponential distribution q-Weibull distribution

Probability distributions

List

Discrete univariate with finite support	Benford Bernoulli beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support	beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval	arcsine ARGUS Balding–Nichols Bates beta beta rectangular Irwin–Hall Kumaraswamy logit-normal noncentral beta raised cosine reciprocal triangular U-quadratic uniform Wigner semicircle

Continuous univariate supported on a semi-infinite interval	Benini Benktander 1st kind Benktander 2nd kind beta prime Burr chi-squared chi Dagum Davis exponential-logarithmic Erlang exponential F folded normal Flory–Schulz Fréchet gamma gamma/Gompertz generalized inverse Gaussian Gompertz half-logistic half-normal Hotelling's T-squared hyper-Erlang hyperexponential hypoexponential inverse chi-squared scaled inverse chi-squared inverse Gaussian inverse gamma Kolmogorov Lévy log-Cauchy log-Laplace log-logistic log-normal Lomax matrix-exponential Maxwell–Boltzmann Maxwell–Jüttner Mittag-Leffler Nakagami noncentral chi-squared Pareto phase-type poly-Weibull Rayleigh relativistic Breit–Wigner Rice shifted Gompertz truncated normal type-2 Gumbel Weibull Discrete Weibull Wilks's lambda

Continuous univariate supported on the whole real line	Cauchy exponential power Fisher's z Gaussian q generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson's S_U Landau Laplace asymmetric Laplace logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel Tracy–Widom variance-gamma Voigt

Continuous univariate with support whose type varies	generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential q-Weibull shifted log-logistic

Mixed continuous-discrete univariate	rectified Gaussian

Multivariate (joint)	Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet generalized Dirichlet multivariate normal multivariate stable multivariate t normal-inverse-gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional	Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped asymmetric Laplace wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular	Degenerate Dirac delta function Singular Cantor

Families	Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia - version of the 4/16/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.