Variation of information
In probability theory and information theory, the variation of information or shared information distance is a measure of the distance between two clusterings (partitions of elements). It is closely related to mutual information; indeed, it is a simple linear expression involving the mutual information. Unlike the mutual information, however, the variation of information is a true metric, in that it obeys the triangle inequality.[1]
Definition
Suppose we have two partitions and of a set into disjoint subsets, namely , . Let , , , . Then the variation of information between the two partitions is:
- .
This is equivalent to the shared information distance between the random variables i and j with respect to the uniform probability measure on defined by for .
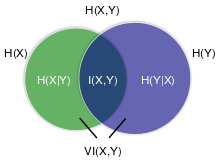
Identities
The variation of information satisfies
- ,
where is the entropy of , and is mutual information between and with respect to the uniform probability measure on . This can be rewritten as
- ,
where is the joint entropy of and , or
- ,
where and are the respective conditional entropies.
References
- ↑ Alexander Kraskov, Harald Stögbauer, Ralph G. Andrzejak, and Peter Grassberger, "Hierarchical Clustering Based on Mutual Information", (2003) ArXiv q-bio/0311039
Further reading
- Arabie, P.; Boorman, S. A. (1973). "Multidimensional scaling of measures of distance between partitions". Journal of Mathematical Psychology. 10: 148–203. doi:10.1016/0022-2496(73)90012-6.
- Meila, Marina (2003). "Comparing Clusterings by the Variation of Information". Learning Theory and Kernel Machines: 173–187. doi:10.1007/978-3-540-45167-9_14.
- Meila, M. (2007). "Comparing clusterings—an information based distance". Journal of Multivariate Analysis. 98 (5): 873–895. doi:10.1016/j.jmva.2006.11.013.
- Kingsford, Carl (2009). "Information Theory Notes" (PDF). Retrieved 22 September 2009.