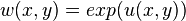Tzitzeica equation

The Tzitzeica equation is a nonlinear partial differential equation devised by Gheorghe Țițeica in 1907 in the study of differential geometry, describing surfaces of constant affine curvature.^[1] The Tzitzeica equation has also been used in nonlinear physics, being an integrable 1+1 dimensional Lorentz invariant system.^[2]

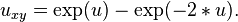
$u_{xy}=\exp(u)-\exp(-2*u).$

On substituting

w(x, y) = exp(u(x, y))

the equation becomes

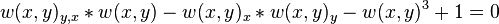
$w(x, y)_{y, x}*w(x, y)-w(x, y)_{x}*w(x, y)_{y}-w(x, y)^3+1 = 0$

Obtain the traveling solution of the original equation by the reverse transformation 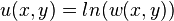$u(x,y)=ln(w(x,y))$ .

References

↑ G. Tzitz´eica, “Geometric infinitesimale-sur une nouvelle classes de surfaces,”Comptes Rendus de l’Acad´emie des Sciences, vol. 144, pp. 1257–1259, 1907.
↑ Andrei D. Polyanin,Valentin F. Zaitsev, HANDBOOK OF NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS, SECOND EDITION p540-542 CRC PRESS

Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential Equations Academy Press
Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
Dongming Wang, Elimination Practice,Imperial College Press 2004
David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759

This article is issued from Wikipedia - version of the 5/17/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.