Tetradecagon
| Regular tetradecagon | |
|---|---|
 A regular tetradecagon | |
| Type | Regular polygon |
| Edges and vertices | 14 |
| Schläfli symbol | {14}, t{7} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D14), order 2×14 |
| Internal angle (degrees) | ≈154.2857° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon.
Regular tetradecagon
A regular tetradecagon has Schläfli symbol {14} and can be constructed as a quasiregular truncated heptagon, t{7}, which alternates two types of edges.
The area of a regular tetradecagon of side length a is given by
Construction
As 14 = 2 × 7, a regular tetradecagon cannot be constructed using a compass and straightedge.[1] However, it is constructible using neusis, as for example in the following illustration with use of the angle trisector.[2]

according to Andrew M. Gleason,[2] based on the angle trisection by means of the Tomahawk.
The animation below gives an approximation of about 0.05° on the center angle:

Construction of an approximated regular tetradecagon
Another possible animation of an approximate construction, also possible with using straightedge and compass.

Based on the unit circle r = 1 [unit of length]
- Constructed side lenght of the tetradecagon in GeoGebra = 0.445041867912629... [unit of length]
- Side lenght of the tetradecagon = = 0.4450418679126288089... [unit of length]
- Absolute error of the constructed side lenght = 1.911...E-16 [unit of length]
- Constructed central angle of the tetradecagon in GeoGebra = 25.714285714285705...°
- Central angle of the tetradecagon = = 25.714285714285714285...°
- Absolute error of the constructed central angle = -9.285...E-15°
Example to illustrate the error
- At a radius r = 1 billion km (the light would need about 55 min for this distance) the absolute error of the side length constructed would be approx. 0.2 mm.
For details, see: Wikibooks: Tetradecagon, construction description (German)
Symmetry

The regular tetradecagon has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1.
These 8 symmetries can be seen in 10 distinct symmetries on the tetradecagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order.[3] Full symmetry of the regular form is r28 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g14 subgroup has no degrees of freedom but can seen as directed edges.
The highest symmetry irregular tetradecagons are d14, a isogonal dotetradecagon constructed by five mirrors which can alternate long and short edges, and p14, an isotoxal tetradecagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular tetradecagon.
Numismatic use
The regular tetradecagon is used as the shape of some commemorative gold and silver Malaysian coins, the number of sides representing the 14 states of the Malaysian Federation.[4]
Related figures
A tetradecagram is a 14-sided star polygon, represented by symbol {14/n}. There are two regular star polygons: {14/3} and {14/5}, using the same vertices, but connecting every third or fifth points. There are also three compounds: {14/2} is reduced to 2{7} as two heptagons, while {14/4} and {14/6} are reduced to 2{7/2} and 2{7/3} as two different heptagrams, and finally {14/7} is reduced to seven digons.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Form | Regular | Compound | Star polygon | Compound | Star polygon | Compound | |
| Image |  {14/1} = {14} |
.svg.png) {14/2} = 2{7} |
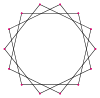 {14/3} |
.svg.png) {14/4} = 2{7/2} |
 {14/5} |
.svg.png) {14/6} = 2{7/3} |
.svg.png) {14/7} or 7{2} |
| Internal angle | ≈154.286° | ≈128.571° | ≈102.857° | ≈77.1429° | ≈51.4286° | ≈25.7143° | 0° |
Deeper truncations of the regular heptagon and heptagrams can produce isogonal (vertex-transitive) intermediate tetradecagram forms with equally spaced vertices and two edge lengths. Other truncations can form double covering polyons 2{p/q}, namely: t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2}, and t{7/2}={14/2}=2{7}.[5]
| Quasiregular | Isogonal | Quasiregular Double covering | ||
|---|---|---|---|---|
 t{7}={14} |
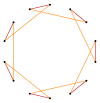 |
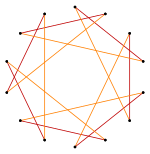 |
 |
 {7/6}={14/6} =2{7/3} |
 t{7/3}={14/3} |
 |
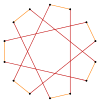 |
 |
 t{7/4}={14/4} =2{7/2} |
 t{7/5}={14/5} |
 |
 |
 |
 t{7/2}={14/2} =2{7} |
Petrie polygons
Regular skew tetradecagons exist as Petrie polygon for many higher-dimensional polytopes, shown in these skew orthogonal projections, including:
| B7 | 2I2(7) (4D) | |||
|---|---|---|---|---|
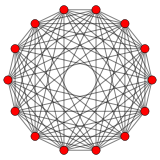 7-orthoplex |
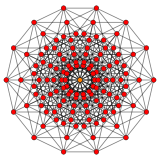 7-cube |
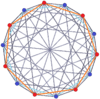 7-7 duopyramid |
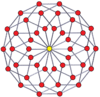 7-7 duoprism |
|
| A13 | D8 | E8 | ||
 13-simplex |
 511 |
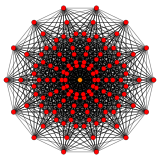 151 |
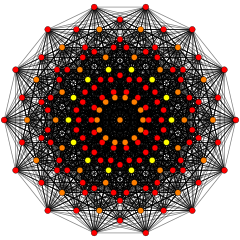 421 |
 241 |
References
- ↑ Wantzel, Pierre (1837). "Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas". Journal de Mathématiques: 366–372.
- 1 2 Gleason, Andrew Mattei (March 1988). "Angle trisection, the heptagon, p. 186 (Fig.1) –187" (PDF). The American Mathematical Monthly. 95 (3): 185–194. doi:10.2307/2323624. Archived from the original (PDF) on 2015-12-19.
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ↑ The Numismatist, Volume 96, Issues 7-12, Page 1409, American Numismatic Association, 1983.
- ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum