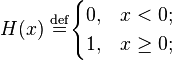Singular measure
In mathematics, two positive (or signed or complex) measures μ and ν defined on a measurable space (Ω, Σ) are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A. This is denoted by 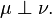
A refined form of Lebesgue's decomposition theorem decomposes a singular measure into a singular continuous measure and a discrete measure. See below for examples.
Examples on Rn
As a particular case, a measure defined on the Euclidean space Rn is called singular, if it is singular in respect to the Lebesgue measure on this space. For example, the Dirac delta function is a singular measure.
Example. A discrete measure.
The Heaviside step function on the real line,
has the Dirac delta distribution 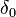 as its distributional derivative. This is a measure on the real line, a "point mass" at 0. However, the Dirac measure
as its distributional derivative. This is a measure on the real line, a "point mass" at 0. However, the Dirac measure 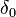 is not absolutely continuous with respect to Lebesgue measure
is not absolutely continuous with respect to Lebesgue measure 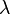 , nor is
, nor is 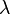 absolutely continuous with respect to
absolutely continuous with respect to 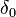 :
: 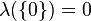 but
but 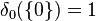 ; if
; if 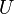 is any open set not containing 0, then
is any open set not containing 0, then 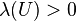 but
but 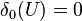 .
.
Example. A singular continuous measure.
The Cantor distribution has a cumulative distribution function that is continuous but not absolutely continuous, and indeed its absolutely continuous part is zero: it is singular continuous.
See also
References
- Eric W Weisstein, CRC Concise Encyclopedia of Mathematics, CRC Press, 2002. ISBN 1-58488-347-2.
- J Taylor, An Introduction to Measure and Probability, Springer, 1996. ISBN 0-387-94830-9.
This article incorporates material from singular measure on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.