Simple precedence parser

In computer science, a simple precedence parser is a type of bottom-up parser for context-free grammars that can be used only by simple precedence grammars.

The implementation of the parser is quite similar to the generic bottom-up parser. A stack is used to store a viable prefix of a sentential form from a rightmost derivation. Symbols , 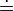and are used to identify the pivot, and to know when to Shift or when to Reduce.

Implementation

• Compute the Wirth–Weber precedence relationship table.
• Start with a stack with only the starting marker $.
• Start with the string being parsed (Input) ended with an ending marker $.
• While not (Stack equals to $S and Input equals to $) (S = Initial symbol of the grammar)
  • Search in the table the relationship between Top(stack) and NextToken(Input)
  • if the relationship is 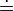or
    • Shift:
    • Push(Stack, relationship)
    • Push(Stack, NextToken(Input))
    • RemoveNextToken(Input)
  • if the relationship is
    • Reduce:
    • SearchProductionToReduce(Stack)
    • RemovePivot(Stack)
    • Search in the table the relationship between the Non terminal from the production and first symbol in the stack (Starting from top)
    • Push(Stack, relationship)
    • Push(Stack, Non terminal)

SearchProductionToReduce (Stack)

• search the Pivot in the stack the nearest from the top
• search in the productions of the grammar which one have the same right side than the Pivot

Example

Given the language:

E  --> E + T' | T'
T' --> T
T  --> T * F  | F
F  --> ( E' ) | num
E' --> E

num is a terminal, and the lexer parse any integer as num.

and the Parsing table:

	E	E'	T	T'	F	+	*	(	)	num	$
E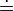
E'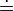
T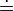
T'
F
+
*
(
)
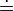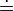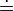num
$

STACK                   PRECEDENCE    INPUT            ACTION

$                            <        2 * ( 1 + 3 )$   SHIFT
$ < 2                        >        * ( 1 + 3 )$     REDUCE (F -> num)
$ < F                        >        * ( 1 + 3 )$     REDUCE (T -> F)
$ < T                        =        * ( 1 + 3 )$     SHIFT
$ < T = *                    <        ( 1 + 3 )$       SHIFT
$ < T = * < (                <        1 + 3 )$         SHIFT
$ < T = * < ( < 1            >        + 3 )$           REDUCE 4 times (F -> num) (T -> F) (T' -> T) (E ->T ') 
$ < T = * < ( < E            =        + 3 )$           SHIFT
$ < T = * < ( < E = +        <        3 )$             SHIFT
$ < T = * < ( < E = + < 3    >        )$               REDUCE 3 times (F -> num) (T -> F) (T' -> T) 
$ < T = * < ( < E = + = T    >        )$               REDUCE 2 times (E -> E + T) (E' -> E)
$ < T = * < ( < E'           =        )$               SHIFT
$ < T = * < ( = E' = )       >        $                REDUCE (F -> ( E' ))
$ < T = * = F                >        $                REDUCE (T -> T * F)
$ < T                        >        $                REDUCE 2 times (T' -> T) (E -> T')
$ < E                        >        $                ACCEPT

References

• Alfred V. Aho, Jeffrey D. Ullman (1977). Principles of Compiler Design. 1st Edition. Addison–Wesley.
• William A. Barrett, John D. Couch (1979). Compiler construction: Theory and Practice. Science Research Associate.
• Jean-Paul Tremblay, P. G. Sorenson (1985). The Theory and Practice of Compiler Writing. McGraw–Hill.