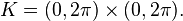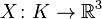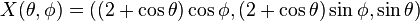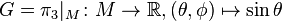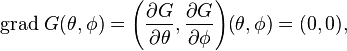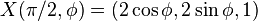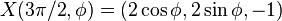Round function

"Round function" may also refer to rounding.

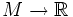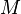In topology and in calculus, a round function is a scalar function M\to{\mathbb{R}}, over a manifold M, whose critical points form one or several connected components, each homeomorphic to the circle 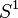S^1, also called critical loops. They are special cases of Morse-Bott functions.

The black circle in one of this critical loops.

For instance

For example, let 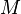M be the torus. Let

K=(0,2\pi)\times(0,2\pi).\,

Then we know that a map

X\colon K\to{\mathbb{R}}^3\,

given by

X(\theta,\phi)=((2+\cos\theta)\cos\phi,(2+\cos\theta)\sin\phi,\sin\theta)\,

is a parametrization for almost all of 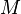M. Now, via the projection 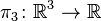\pi_3\colon{\mathbb{R}}^3\to{\mathbb{R}} we get the restriction

G=\pi_3|_M\colon M\to{\mathbb{R}}, (\theta,\phi) \mapsto \sin \theta \,

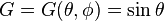G=G(\theta,\phi)=\sin\theta is a function whose critical sets are determined by

{\rm grad}\ G(\theta,\phi)= \left({{\partial}G\over {\partial}\theta},{{\partial}G\over {\partial}\phi}\right)\!\left(\theta,\phi\right)=(0,0),\,

this is if and only if 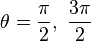\theta={\pi\over 2},\ {3\pi\over 2}.

These two values for 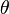\theta give the critical sets

X({\pi/2},\phi)=(2\cos\phi,2\sin\phi,1)\,
X({3\pi/2},\phi)=(2\cos\phi,2\sin\phi,-1)\,

which represent two extremal circles over the torus 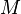M.

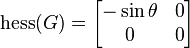
Observe that the Hessian for this function is

{\rm hess}(G)= \begin{bmatrix} -\sin\theta & 0 \\ 0 & 0 \end{bmatrix}

which clearly it reveals itself as rank of 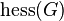{\rm hess}(G) equal to one at the tagged circles, making the critical point degenerate, that is, showing that the critical points are not isolated.

Round complexity

Mimicking the L–S category theory one can define the round complexity asking for whether or not exist round functions on manifolds and/or for the minimum number of critical loops.

References

This article is issued from Wikipedia - version of the 2/10/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.