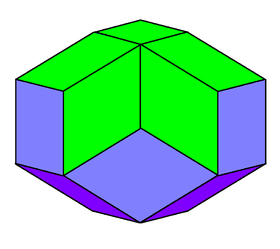
Rhombic icosahedron
| Rhombic icosahedron | |
|---|---|
 | |
| Type | Zonohedron |
| Faces | 20 rhombi |
| Edges | 40 |
| Vertices | 22 |
| Faces per vertex | 3, 4 and 5 |
| Dual polyhedron | Irregular-faced pentagonal gyrobicupola |
| Symmetry | D5d, [2+,10], (2*5) |
| Properties | convex, zonohedron |
A rhombic icosahedron (or rhombic icosacontahedron) is a polyhedron shaped like an oblate sphere. It can be derived from the rhombic triacontahedron by removing 10 middle faces.

It is composed of 20 rhombic faces, of which three, four, or five meet at each vertex. It has 10 faces on the axis of symmetry with 10 rhombi following the equator.
Even though all the faces are congruent, the rhombic icosahedron is not face-transitive, since one may distinguish whether a particular face is near the equator or a pole by examining the types of vertices surrounding that face.
The rhombic icosahedron is a zonohedron that is dual to an irregular-faced pentagonal gyrobicupola.

It has D5d, [2+,10], (2*5) symmetry, order 20.
The rhombic icosahedron forms the convex hull of the vertex-first projection of a 5-cube to 3 dimensions. This is the same way one can obtain a rhombic dodecahedron from a 4-cube and a rhombic triacontahedron from a 6-cube.