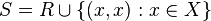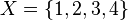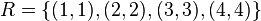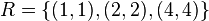Reflexive closure
In mathematics, the reflexive closure of a binary relation R on a set X is the smallest reflexive relation on X that contains R.
For example, if X is a set of distinct numbers and x R y means "x is less than y", then the reflexive closure of R is the relation "x is less than or equal to y".
Definition
The reflexive closure S of a relation R on a set X is given by
In words, the reflexive closure of R is the union of R with the identity relation on X.
Example
As an example, if
then the relation 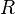 is already reflexive by itself, so it doesn't differ from its reflexive closure.
is already reflexive by itself, so it doesn't differ from its reflexive closure.
However, if any of the pairs in 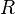 was absent, it would be inserted for the reflexive closure.
For example, if
was absent, it would be inserted for the reflexive closure.
For example, if
then reflexive closure is, by the definition of a reflexive closure:
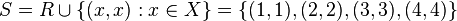 .
.
See also
References
- Franz Baader and Tobias Nipkow, Term Rewriting and All That, Cambridge University Press, 1998, p. 8
This article is issued from Wikipedia - version of the 3/17/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.