Rastrigin function
Rastrigin function of two variables

In 3D

Contour
In mathematical optimization, the Rastrigin function is a non-convex function used as a performance test problem for optimization algorithms. It is a typical example of non-linear multimodal function. It was first proposed by Rastrigin [1] as a 2-dimensional function and has been generalized by Mühlenbein et al.[2] Finding the minimum of this function is a fairly difficult problem due to its large search space and its large number of local minima.
It is defined by:
where 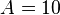 and
and ![x_i\in[-5.12,5.12]](../I/m/89f8f3dc16012a185e5a31ec62c919e5.png) . It has a global minimum at
. It has a global minimum at  where
where  .
.
See also
Notes
- ↑ Rastrigin, L. A. "Systems of extremal control." (1974).
- ↑ H. Mühlenbein, D. Schomisch and J. Born. "The Parallel Genetic Algorithm as Function Optimizer ". Parallel Computing, 17, pages 619–632, 1991.
This article is issued from Wikipedia - version of the 9/3/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![f(\mathbf{x}) = A n + \sum_{i=1}^n \left[x_i^2 - A\cos(2 \pi x_i)\right]](../I/m/5831f65c6b1d64c2cf83d8eac84e1c3c.png)