Quot scheme
In algebraic geometry, the Quot scheme is a scheme parametrizing locally free sheaves on a projective scheme. More specifically, if X is a projective scheme over a Noetherian scheme S and if F is a coherent sheaf on X, then there is a scheme 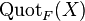 whose set of T-points
whose set of T-points 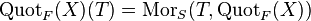 is the set of isomorphism classes of the quotients of
is the set of isomorphism classes of the quotients of 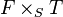 that are flat over T. The notion was introduced by Alexander Grothendieck.[1]
that are flat over T. The notion was introduced by Alexander Grothendieck.[1]
It is typically used to construct another scheme parametrizing geometric objects that are of interest such as a Hilbert scheme. (In fact, taking F to be the structure sheaf 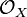 gives a Hilbert scheme.)
gives a Hilbert scheme.)
References
- ↑ Grothendieck, Alexander. Techniques de construction et théorèmes d'existence en géométrie algébrique III : préschémas quotients. Séminaire Bourbaki, 6 (1960-1961), Exposé No. 212, 20 p.
- Nitsure, N. Construction of Hilbert and Quot schemes. Fundamental algebraic geometry: Grothendieck’s FGA explained, Mathematical Surveys and Monographs 123, American Mathematical Society 2005, 105–137.
- https://amathew.wordpress.com/2012/06/02/the-stack-of-coherent-sheaves/
This article is issued from Wikipedia - version of the 5/4/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.