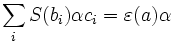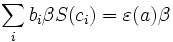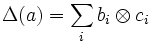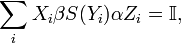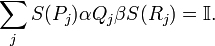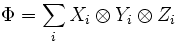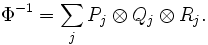Quasi-Hopf algebra

A quasi-Hopf algebra is a generalization of a Hopf algebra, which was defined by the Russian mathematician Vladimir Drinfeld in 1989.

A quasi-Hopf algebra is a quasi-bialgebra 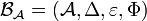\mathcal{B_A} = (\mathcal{A}, \Delta, \varepsilon, \Phi) for which there exist 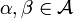\alpha, \beta \in \mathcal{A} and a bijective antihomomorphism S (antipode) of 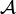\mathcal{A} such that

\sum_i S(b_i) \alpha c_i = \varepsilon(a) \alpha
\sum_i b_i \beta S(c_i) = \varepsilon(a) \beta

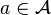for all a \in \mathcal{A} and where

\Delta(a) = \sum_i b_i \otimes c_i

and

\sum_i X_i \beta S(Y_i) \alpha Z_i = \mathbb{I},
\sum_j S(P_j) \alpha Q_j \beta S(R_j) = \mathbb{I}.

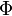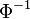where the expansions for the quantities \Phiand \Phi^{-1} are given by

\Phi = \sum_i X_i \otimes Y_i \otimes Z_i

and

\Phi^{-1}= \sum_j P_j \otimes Q_j \otimes R_j.

As for a quasi-bialgebra, the property of being quasi-Hopf is preserved under twisting.

Usage

Quasi-Hopf algebras form the basis of the study of Drinfeld twists and the representations in terms of F-matrices associated with finite-dimensional irreducible representations of quantum affine algebra. F-matrices can be used to factorize the corresponding R-matrix. This leads to applications in Statistical mechanics, as quantum affine algebras, and their representations give rise to solutions of the Yang-Baxter equation, a solvability condition for various statistical models, allowing characteristics of the model to be deduced from its corresponding quantum affine algebra. The study of F-matrices has been applied to models such as the Heisenberg XXZ model in the framework of the algebraic Bethe ansatz. It provides a framework for solving two-dimensional integrable models by using the Quantum inverse scattering method.

See also

References

This article is issued from Wikipedia - version of the 9/15/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.