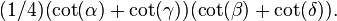Perpendicular bisector construction of a quadrilateral

In geometry, the perpendicular bisector construction of a quadrilateral is a construction which produces a new quadrilateral from a given quadrilateral using the perpendicular bisectors to the sides of the former quadrilateral. This construction arises naturally in an attempt to find a replacement for the circumcenter of a quadrilateral in the case that is non-cyclic.

Definition of the construction

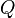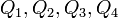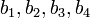Suppose that the vertices of the quadrilateral $Q$ are given by $Q_1,Q_2,Q_3,Q_4$ . Let $b_1,b_2,b_3,b_4$ be the perpendicular bisectors of sides 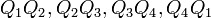$Q_1Q_2,Q_2Q_3,Q_3Q_4,Q_4Q_1$ respectively. Then their intersections 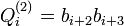$Q_i^{(2)}=b_{i+2}b_{i+3}$ , with subscripts considered modulo 4, form the consequent quadrilateral 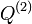$Q^{(2)}$ . The construction is then iterated on 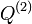$Q^{(2)}$ to produce 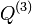$Q^{(3)}$ and so on.

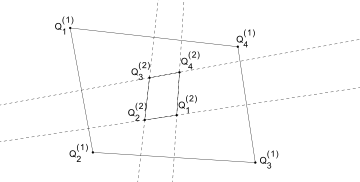
First iteration of the perpendicular bisector construction

An equivalent construction can be obtained by letting the vertices of 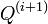$Q^{(i+1)}$ be the circumcenters of the 4 triangles formed by selecting combinations of 3 vertices of $Q^{(i)}$ .

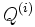Properties

1. If 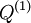$Q^{(1)}$ is not cyclic, then 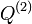$Q^{(2)}$ is not degenerate.^[1]

2. Quadrilateral 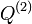$Q^{(2)}$ is never cyclic.^[1] Combining #1 and #2, 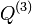$Q^{(3)}$ is always nondegenrate.

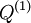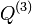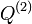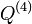3. Quadrilaterals $Q^{(1)}$ and $Q^{(3)}$ are homothetic, and in particular, similar.^[2] Quadrilaterals $Q^{(2)}$ and $Q^{(4)}$ are also homothetic.

3. The perpendicular bisector construction can be reversed via isogonal conjugation.^[3] That is, given 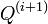$Q^{(i+1)}$ , it is possible to construct $Q^{(i)}$ .

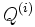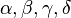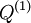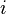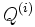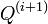4. Let $\alpha, \beta, \gamma, \delta$ be the angles of $Q^{(1)}$ . For every $i$ , the ratio of areas of $Q^{(i)}$ and $Q^{(i+1)}$ is given by^[3]

(1/4)(\cot(\alpha)+\cot(\gamma))(\cot(\beta)+\cot(\delta)).

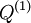5. If $Q^{(1)}$ is convex then the sequence of quadrilaterals 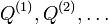$Q^{(1)}, Q^{(2)},\ldots$ converges to the isoptic point of 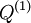$Q^{(1)}$ , which is also the isoptic point for every 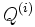$Q^{(i)}$ . Similarly, if 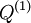$Q^{(1)}$ is concave, then the sequence 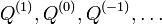$Q^{(1)}, Q^{(0)}, Q^{(-1)},\ldots$ obtained by reversing the construction converges to the Isoptic Point of the 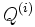$Q^{(i)}$ 's.^[3]

References

↑ 1.0 1.1 J. King, Quadrilaterals formed by perpendicular bisectors, in Geometry Turned On, (ed. J. King), MAA Notes 41, 1997, pp. 29–32.
↑ G. C. Shephard, The perpendicular bisector construction, Geom. Dedicata, 56 (1995) 75–84.
↑ 3.0 3.1 3.2 O. Radko and E. Tsukerman, The Perpendicular Bisector Construction, the Isoptic Point and the Simson Line of a Quadrilateral, Forum Geometricorum 12: 161–189 (2012).

J. Langr, Problem E1050, Amer. Math. Monthly, 60 (1953) 551.
V. V. Prasolov, Plane Geometry Problems, vol. 1 (in Russian), 1991; Problem 6.31.
V. V. Prasolov, Problems in Plane and Solid Geometry, vol. 1 (translated by D. Leites), available at http://students.imsa.edu/~tliu/math/planegeo.eps.
D. Bennett, Dynamic geometry renews interest in an old problem, in Geometry Turned On, (ed. J. King), MAA Notes 41, 1997, pp. 25–28.
J. King, Quadrilaterals formed by perpendicular bisectors, in Geometry Turned On, (ed. J. King), MAA Notes 41, 1997, pp. 29–32.
G. C. Shephard, The perpendicular bisector construction, Geom. Dedicata, 56 (1995) 75–84.
A. Bogomolny, Quadrilaterals formed by perpendicular bisectors, Interactive Mathematics Miscellany and Puzzles, http://www.cut-the-knot.org/Curriculum/Geometry/PerpBisectQuadri.shtml.
B. Grünbaum, On quadrangles derived from quadrangles—Part 3, Geombinatorics 7(1998), 88–94.
O. Radko and E. Tsukerman, The Perpendicular Bisector Construction, the Isoptic Point and the Simson Line of a Quadrilateral, Forum Geometricorum 12: 161–189 (2012).

This article is issued from Wikipedia - version of the 4/12/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.