Moss's Egg
Moss's Egg
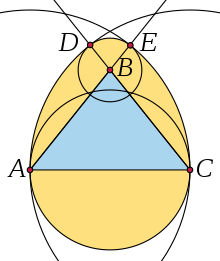
In Euclidean geometry, Moss's Egg is an oval made by smoothly connecting four circular arcs. It can be constructed from any isosceles triangle ABC with apex B, as long as the angle at B is less than 60°; often, ABC is an isosceles right triangle. Draw a semicircle on the base AC of the triangle, outside of the triangle. Connect it to a circular arc centered at C from A to a point D on line BC, and by another circular arc centered at A from C to a point E on line AB. When the apex angle at B is less than 60°, these two points D and E will be outside the triangle, equidistant from B. Complete the oval by a circular arc centered at B, from D to E.[1][2][3]
References
- ↑ Dixon, R (1991). Mathographics. Dover. p. 5.
- ↑ Weisstein, Eric. "Math World". Wolfram MathWorld. Wolfram Math World. Retrieved 19 August 2015.
- ↑ Hreinsdóttir, Freyja. "Euclidean Eggs" (PDF). Retrieved 19 August 2015.
This article is issued from Wikipedia - version of the 11/27/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.