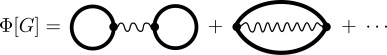Luttinger–Ward functional
In solid state physics, the Luttinger–Ward functional,[1] proposed by Joaquin Mazdak Luttinger and John Clive Ward in 1960,[2] is a scalar functional of the bare electron-electron interaction and the renormalized many-body Green's function. In terms of Feynman diagrams, the Luttinger–Ward functional is the sum of all closed, bold, two-particle irreducible diagrams, i.e., all diagrams without particles going in or out that do not fall apart if one removes two propagator lines. It is usually written as , where is the Green's function.
The Luttinger–Ward functional has no direct physical meaning, but it is useful in proving conservation laws.
The functional is related to the Baym–Kadanoff functional,[3] constructed by Gordon Baym and Leo Kadanoff in 1961, which is the effective two-particle irreducible action.[4]
Construction
Given a system characterized by the action in terms of Grassmann fields , the partition function can be expressed as the path integral:
- ,
where is a binary source field. By expansion in the Dyson series, one finds that is the sum of all (possibly disconnected), closed Feynman diagrams. in turn is the generating functional of the N-particle Green's function:
The linked-cluster theorem asserts that the effective action is the sum of all closed, connected (“0-particle irreducible”) diagrams. in turn is the generating functional for the connected Green's function. As an example, the two particle connected Green's function reads:
To pass to the two-particle irreducible (2PI) effective action, one performs a Legendre transform of to a new binary source field. One chooses an, at this point arbitrary, convex as the source and obtains the functional:
- with .
Unlike the connected case, one more step is required to obtain a generating functional from the two-particle irreducible effective action because of the presence of a non-interacting part. By subtracting it, one obtains the Luttinger–Ward functional:[5]
Along the lines of the proof of the linked-cluster theorem, one can show that this is the generating functional for the two-particle irreducible propagators.
Properties
Diagrammatically, the Luttinger–Ward functional is the sum of all closed, bold, two-particle irreducible Feynman diagrams (also known as “skeleton” diagrams):
The diagrams are closed as they do not have any external legs, i.e., no particles going in or out of the diagram. They are “bold” because they are formulated in terms of the interacting or bold propagator rather than the non-interacting one. They are two-particle irreducible since they do not become disconnected if we sever up to two fermionic lines.
The Luttinger–Ward functional is related to the grand potential of a system:
is a generating functional for irreducible vertex quantities: the first functional derivative with respect to gives the self-energy, while the second derivative gives the partially two-particle irreducible four-point vertex:
- ;
While the Luttinger–Ward functional exists, it can be shown to be not unique for Hubbard-like models.[6] In particular, the irreducible vertex functions show a set of divergencies, which causes the self-energy to bifurcate into a causal and a non-causal (and thus unphysical) solution.[7] However, by restricting the self-energy to causal solutions, one can restore uniqueness of the functional.
See also
References
- ↑ Potthoff, M. (2003). "Self-energy-functional approach to systems of correlated electrons". European Physical Journal B. 32 (4): 429–436. doi:10.1140/epjb/e2003-00121-8.
- ↑ Luttinger, J. M.; Ward, J. C. (1960). "Ground-State Energy of a Many-Fermion System. II". Physical Review. 118 (5): 1417–1427. doi:10.1103/PhysRev.118.1417.
- ↑ Kotliar, G.; Savrasov, S. Y.; Haule, K.; Oudovenko, V. S.; Parcollet, O.; Marianetti, C. A. (2006). "Electronic structure calculations with dynamical mean-field theory". Rev. Mod. Phys. 78 (3): 865–951. doi:10.1103/RevModPhys.78.865.
- ↑ Baym, G.; Kadanoff, L. P. (1961). "Conservation Laws and Correlation Functions". Physical Review. 124 (2): 287–299. doi:10.1103/PhysRev.124.287.
- ↑ Rentrop, J. F.; Meden, V.; Jakobs, S. G. (2016). "Renormalization group flow of the Luttinger–Ward functional: Conserving approximations and application to the Anderson impurity model". Phys. Rev. B. 93 (19): 195160. doi:10.1103/PhysRevB.93.195160.
- ↑ Kozik, E.; Ferrero, M.; Georges, A. (2015). "Nonexistence of the Luttinger-Ward Functional and Misleading Convergence of Skeleton Diagrammatic Series for Hubbard-Like Models". Phys. Rev. Lett. 114 (15): 156402. doi:10.1103/PhysRevLett.114.156402.
- ↑ Schaefer, T.; Rohringer, G.; Gunnarsson, O.; Ciuchi, S.; Sangiovanni, G.; Toschi, A. (2013). "Divergent Precursors of the Mott-Hubbard Transition at the Two-Particle Level". Phys. Rev. Lett. 110 (24): 246405. doi:10.1103/PhysRevLett.110.246405.