Loop theorem
In mathematics, in the topology of 3-manifolds, the loop theorem is a generalization of Dehn's lemma. The loop theorem was first proven by Christos Papakyriakopoulos in 1956, along with Dehn's lemma and the Sphere theorem.
A simple and useful version of the loop theorem states that if there is a map
with 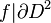 not nullhomotopic in
not nullhomotopic in 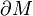 , then there is an embedding with the same property.
, then there is an embedding with the same property.
The following version of the loop theorem, due to John Stallings, is given in the standard 3-manifold treatises (such as Hempel or Jaco):
Let 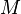 be a 3-manifold and let
be a 3-manifold and let 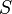 be a connected surface in
be a connected surface in 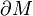 . Let
. Let 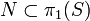 be a normal subgroup such that
be a normal subgroup such that 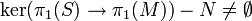 .
Let
.
Let
be a continuous map such that
and
Then there exists an embedding
such that
and
Furthermore if one starts with a map f in general position, then for any neighborhood U of the singularity set of f, we can find such a g with image lying inside the union of image of f and U.
Stalling's proof utilizes an adaptation, due to Whitehead and Shapiro, of Papakyriakopoulos' "tower construction". The "tower" refers to a special sequence of coverings designed to simplify lifts of the given map. The same tower construction was used by Papakyriakopoulos to prove the sphere theorem (3-manifolds), which states that a nontrivial map of a sphere into a 3-manifold implies the existence of a nontrivial embedding of a sphere. There is also a version of Dehn's lemma for minimal discs due to Meeks and S.-T. Yau, which also crucially relies on the tower construction.
A proof not utilizing the tower construction exists of the first version of the loop theorem. This was essentially done 30 years ago by Friedhelm Waldhausen as part of his solution to the word problem for Haken manifolds; although he recognized this gave a proof of the loop theorem, he did not write up a detailed proof. The essential ingredient of this proof is the concept of Haken hierarchy. Proofs were later written up, by Klaus Johannson, Marc Lackenby, and Iain Aitchison with Hyam Rubinstein.
References
- W. Jaco, Lectures on 3-manifolds topology, A.M.S. regional conference series in Math 43.
- J. Hempel, 3-manifolds, Princeton University Press 1976.
- Hatcher, Notes on basic 3-manifold topology, available online
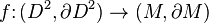
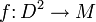
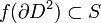
![[f|\partial D^2]\notin N. \,](../I/m/11088215263daf77690a18824a7ac97c.png)
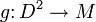
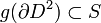
![[g|\partial D^2]\notin N. \,](../I/m/b63a090d728fe15d8b518a670bddda9b.png)