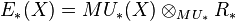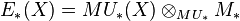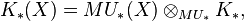Landweber exact functor theorem

In mathematics, the Landweber exact functor theorem, named after Peter Landweber, is a theorem in algebraic topology. It is known that a complex orientation of a homology theory leads to a formal group law. The Landweber exact functor theorem (or LEFT for short) can be seen as a method to reverse this process: it constructs a homology theory out of a formal group law.

Statement

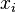The coefficient ring of complex cobordism is $MU_*(*) = MU_* \cong \mathbb{Z}[x_1,x_2,\dots]$ , where the degree of $x_i$ is 2i. This is isomorphic to the graded Lazard ring 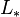$\mathcal{}L_*$ . This means that giving a formal group law F (of degree −2) over a graded ring 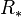$\mathcal{}R_*$ is equivalent to giving a graded ring morphism 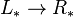$L_*\to R_*$ . Multiplication by an integer n >0 is defined inductively as a power series, by

[n+1]^F x = F(x, [n]^F x)

and

[1]^F x = x.

Let now F be a formal group law over a ring 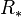$\mathcal{}R_*$ . Define for a topological space X

E_*(X) = MU_*(X)\otimes_{MU_*}R_*

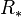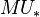Here $\mathcal{}R_*$ gets its $\mathcal{}MU_*$ -algebra structure via F. The question is: is E a homology theory? It is obviously a homotopy invariant functor, which fulfills excision. The problem is that tensoring in general does not preserve exact sequences. One could demand that 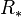$\mathcal{}R_*$ is flat over 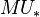$\mathcal{}MU_*$ , but that would be too strong in practice. Peter Landweber found another criterion:

Theorem (Landweber exact functor theorem)

For every prime p, there are elements

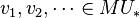v_1,v_2,\cdots \in MU_*

such that we have the following: Suppose that

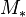\mathcal{}M_*

is a graded

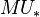\mathcal{}MU_*

-module and the sequence

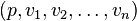(p,v_1,v_2,\dots, v_n)

is regular for M, for every p and n. Then

E_*(X) = MU_*(X)\otimes_{MU_*}M_*

is a homology theory on CW-complexes.

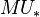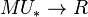In particular, every formal group law F over a ring R yields a module over $\mathcal{}MU_*$ since we get via F a ring morphism $MU_*\to R$ .

Remarks

There is also a version for Brown–Peterson cohomology BP. The spectrum BP is a direct summand of 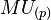$MU_{(p)}$ with coefficients $\mathbb{Z}_{(p)}[v_1,v_2,\dots]$ . The statement of the LEFT stays true if one fixes a prime p and substitutes BP for MU.
The classical proof of the LEFT uses the Landweber–Morava invariant ideal theorem: the only prime ideals of 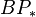$\mathcal{}BP_*$ which are invariant under coaction of 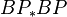$\mathcal{}BP_*BP$ are the 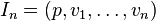$I_n = (p,v_1,\dots, v_n)$ . This allows to check flatness only against the 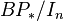$\mathcal{}BP_*/I_n$ (see Landweber, 1976).
The LEFT can be strengthened as follows: let 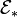$\mathcal{E}_*$ be the (homotopy) category of Landweber exact 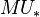$\mathcal{}MU_*$ -modules and 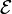$\mathcal{E}$ the category of MU-module spectra M such that 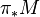$\mathcal{}\pi_*M$ is Landweber exact. Then the functor 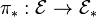$\pi_*:\mathcal{E}\to \mathcal{E}_*$ is an equivalence of categories. The inverse functor (given by the LEFT) takes 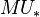$\mathcal{}MU_*$ -algebras to (homotopy) MU-algebra spectra (see Hovey, Strickland, 1999, Thm 2.7).

Examples

The archetypical and first known (non-trivial) example is complex K-theory K. Complex K-theory is complex oriented and has as formal group law 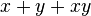$x+y+xy$ . The corresponding morphism 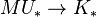$MU_*\to K_*$ is also known as the Todd genus. We have then an isomorphism

K_*(X) = MU_*(X)\otimes_{MU_*}K_*,

called the Conner–Floyd isomorphism.

While complex K-theory was constructed before by geometric means, many homology theories were first constructed via the Landweber exact functor theorem. This includes elliptic homology, the Johnson–Wilson theories 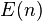$E(n)$ and the Lubin–Tate spectra $E_n$ .

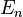While homology with rational coefficients 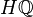$H\mathbb{Q}$ is Landweber exact, homology with integer coefficients 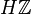$H\mathbb{Z}$ is not Landweber exact. Furthermore, Morava K-theory K(n) is not Landweber exact.

Modern reformulation

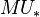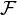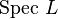A module M over $\mathcal{}MU_*$ is the same as a quasi-coherent sheaf $\mathcal{F}$ over $\text{Spec }L$ , where L is the Lazard ring. If 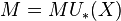$M = \mathcal{}MU_*(X)$ , then M has the extra datum of a 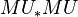$\mathcal{}MU_*MU$ coaction. A coaction on the ring level corresponds to that 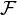$\mathcal{F}$ is an equivariant sheaf with respect to an action of an affine group scheme G. It is a theorem of Quillen that $G \cong \Z[b_1, b_2,\dots]$ and assigns to every ring R the group of power series

g(t) = t+b_1t^2+b_2t^3+\cdots\in R[[t]]

It acts on the set of formal group laws 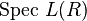$\text{Spec }L(R)$ via

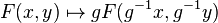F(x,y) \mapsto gF(g^{-1}x, g^{-1}y)

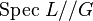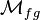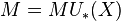These are just the coordinate changes of formal group laws. Therefore, one can identify the stack quotient $\text{Spec }L // G$ with the stack of (1-dimensional) formal groups $\mathcal{M}_{fg}$ and $\mathcal{}M = MU_*(X)$ defines a quasi-coherent sheaf over this stack. Now it is quite easy to see that it suffices that M defines a quasi-coherent sheaf 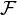$\mathcal{F}$ which is flat over 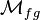$\mathcal{M}_{fg}$ in order that 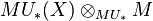$MU_*(X)\otimes_{MU_*}M$ is a homology theory. The Landweber exactness theorem can then be interpreted as a flatness criterion for 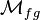$\mathcal{M}_{fg}$ (see Lurie 2010).

Refinements to 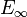$E_\infty$ -ring spectra

While the LEFT is known to produce (homotopy) ring spectra out of 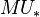$\mathcal{}MU_*$ , it is a much more delicate question to understand when these spectra are actually 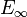$E_\infty$ -ring spectra. As of 2010, the best progress was made by Jacob Lurie. If X is an algebraic stack and 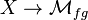$X\to \mathcal{M}_{fg}$ a flat map of stacks, the discussion above shows that we get a presheaf of (homotopy) ring spectra on X. If this map factors over 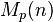$M_p(n)$ (the stack of 1-dimensional p-divisible groups of height n) and the map 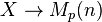$X\to M_p(n)$ is etale, then this presheaf can be refined to a sheaf of 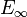$E_\infty$ -ring spectra (see Goerss). This theorem is important for the construction of topological modular forms.

References

P. Goerss, Realizing families of Landweber exact homology theories
Hovey, Mark and Strickland, Neil P., Morava K-theories and localisation, Mem.Amer. Math. Soc., 139 (1999), no. 666.
P. S. Landweber, 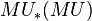$MU_*(MU)$ , American Journal of Mathematics 98 (1976), 591–610.
J. Lurie, Chromatic Homotopy Theory, Lecture Notes (2010)

This article is issued from Wikipedia - version of the 5/14/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.