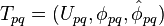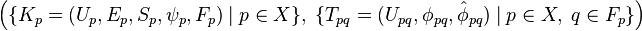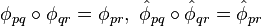Kuranishi structure
In mathematics, especially in topology, a Kuranishi structure is a smooth analogue of scheme structure. If a topological space is endowed with a Kuranishi structure, then locally it can be identified with the zero set of a smooth map 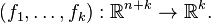 Kuranishi structure was introduced by Japanese mathematicians Kenji Fukaya and Kaoru Ono in the study of Gromov–Witten invariants in symplectic geometry.[1]
Kuranishi structure was introduced by Japanese mathematicians Kenji Fukaya and Kaoru Ono in the study of Gromov–Witten invariants in symplectic geometry.[1]
Definition
Let 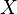 be a compact metrizable topological space. Let
be a compact metrizable topological space. Let 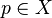 be a point. A Kuranishi neighborhood of
be a point. A Kuranishi neighborhood of 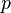 (of dimension
(of dimension 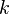 ) is a 5-tuple
) is a 5-tuple
where
-
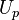 is a smooth orbifold;
is a smooth orbifold; -
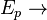 is a smooth orbifold vector bundle;
is a smooth orbifold vector bundle; -
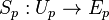 is a smooth section;
is a smooth section; -
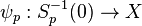 is a continuous map and is homeomorphic onto its image
is a continuous map and is homeomorphic onto its image 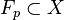 .
.
They should satisfy that 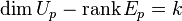 .
.
If 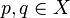 and
and 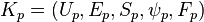 ,
, 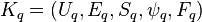 are their Kuranishi neighborhoods respectively, then a coordinate change from
are their Kuranishi neighborhoods respectively, then a coordinate change from 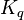 to
to 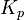 is a triple
is a triple
where
-
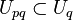 is an open sub-orbifold;
is an open sub-orbifold; -
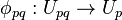 is an orbifold embedding;
is an orbifold embedding; -
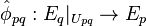 is an orbifold vector bundle embedding which covers
is an orbifold vector bundle embedding which covers 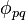 .
.
In addition, they must satisfy the compatibility condition:
-
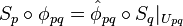 ;
; -
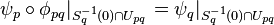 .
.
A Kuranishi structure on 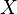 of dimension
of dimension 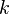 is a collection
is a collection
where
-
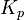 is a Kuranishi neighborhood of
is a Kuranishi neighborhood of 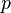 of dimension
of dimension 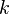 ;
; -
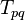 is a coordinate change from
is a coordinate change from 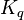 to
to 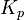 .
.
In addition, the coordinate changes must satisfy the cocycle condition, namely, whenever 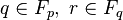 , we require that
, we require that
over the regions where both sides are defined.
History
In Gromov–Witten theory, one needs to define integration over the moduli space of stable maps 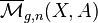 (see for example [2]). They are maps
(see for example [2]). They are maps 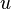 from a nodal Riemann surface with genus
from a nodal Riemann surface with genus 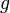 and
and 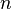 marked points into a symplectic manifold
marked points into a symplectic manifold 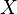 , such that each component satisfies the Cauchy–Riemann equation
, such that each component satisfies the Cauchy–Riemann equation
-
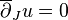 .
.
-
If the moduli space is a smooth, compact, oriented manifold or orbifold, then the integration (or a fundamental class) can be defined. When the symplectic manifold 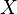 is semi-positive, this is indeed the case (except for codimension 2 boundaries of the moduli space) if the almost complex structure
is semi-positive, this is indeed the case (except for codimension 2 boundaries of the moduli space) if the almost complex structure 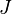 is perturbed generically. However, when
is perturbed generically. However, when 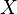 is not semi-positive, the moduli space may contain configurations for which one component is a multiple cover of a holomorphic sphere
is not semi-positive, the moduli space may contain configurations for which one component is a multiple cover of a holomorphic sphere 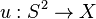 whose intersection with the first Chern class of
whose intersection with the first Chern class of 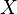 is negative. Such configurations make the moduli space very singular so a fundamental class cannot be defined in the usual way.
is negative. Such configurations make the moduli space very singular so a fundamental class cannot be defined in the usual way.
The notion of Kuranishi structure was a way of defining a virtual fundamental cycle, which plays the same role as a fundamental cycle when the moduli space is cut out transversely. It was first used by Fukaya and Ono in defining the Gromov–Witten invariants and Floer homology, and was further developed when Fukaya, Oh, Ohta, Ono studied the Lagrangian intersection Floer theory.[3]
References
- ↑ Fukaya, K. and Ono, K., "Arnold Conjecture and Gromov–Witten Invariant", Topology 38 (1999), no. 5, 933–1048
- ↑ McDuff, D and Salamon, D. "J-holomorphic curves and symplectic topology", American Mathematical Society Colloquium Publications, 52. American Mathematical Society, Providence, RI, 2004, ISBN 0-8218-3485-1
- ↑ Fukaya, K., Oh, Y.-G., Ohta, H. and Ono, K., "Lagrangian intersection Floer theory: anomaly and obstruction, Part I and Part II", AMS/IP Studies in Advanced Mathematics, 46, American Mathematical Society, Providence, RI; International Press, Somerville, MA, 2009. ISBN 978-0-8218-4836-4