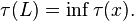Knot thickness

In knot theory, each link and knot can have an assigned knot thickness. Each realization of a link or knot has a thickness assigned to it. The thickness τ of a link allows us to introduce a scale with respect to which we can then define the ropelength of a link.

Definition

There exist several possible definitions of thickness that coincide for smooth enough curves.

Global radius of curvature

The thickness is defined using the simpler concept of the local thickness τ(x). The local thickness at a point x on the link is defined as

\tau(x)=\inf r(x,y,z),\,

where x, y, and z are points on the link, all distinct, and r(x, y, z) is the radius of the circle that passes through all three points (x, y, z). From this definition we can deduce that the local thickness is at most equal to the local radius of curvature.

The thickness of a link is defined as

\tau(L) = \inf \tau(x).[1]

Injectivity radius

This definition ensures that a normal tube to the link with radius equal to τ(L) will not self intersect, and so we arrive at a "real world" knot made out of a thick string.[2]

References

  1. ↑ O. Gonzalez, J.H. Maddocks, "Global Curvature, Thickness and the Ideal Shapes of Knots", Proc. National Academy of Sciences of the USA 96 (1999) 4769-4773
  2. ↑ Thickness of knots R. A. Litherland, J. Simon, O. Durumeric, and E. Rawdon Topology Appl., 91(3): 233-244, 1999.]
This article is issued from Wikipedia - version of the 5/4/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.