Orthoptic (geometry)

In the geometry of curves, an orthoptic is the set of points for which two tangents of a given curve meet at a right angle.

The orthoptic of a parabola is its directrix.

Ellipse and its orthoptic (purple)

Hyperbola with its orthoptic (purple)

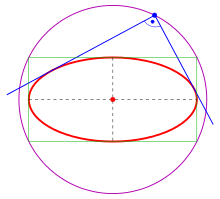
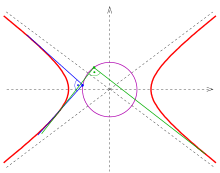
Examples

The orthoptic of

1) a parabola is its directrix (proof: s. parabola),

2) an ellipse

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1

is the director circle

x^{2}+y^{2}=a^{2}+b^{2}

(s. below),

3) a hyperbola

{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\,a>b,

is the circle

x^{2}+y^{2}=a^{2}-b^{2}

(in case of

a\leq b

there are no orthogonal tangents, s. below),

4) an astroid

x^{{2/3}}+y^{{2/3}}=1

is a quadrifolium with the polar equation

r={\tfrac {1}{{\sqrt {2}}}}\cos(2\varphi ),\ 0\leq \varphi <2\pi ,

(s. below).

Generalizations: 1) An isoptic is the set of points for which two tangents of a given curve meet at a fixed angle (s. below).; 2) An isoptic of two plane curves is the set of points for which two tangents meet at a fixed angle.; 3) Thales' theorem on a chord $\overline {P_{1}P_{2}}$ can be considered as the orthoptic of two circles which are degenerated to the two points $P_{1},P_{2}$ .

Remark: In medicine there exists the term orthoptic, too.

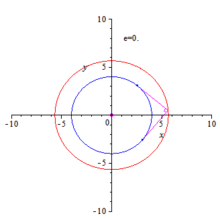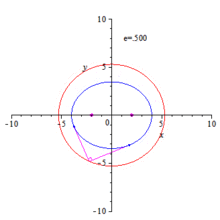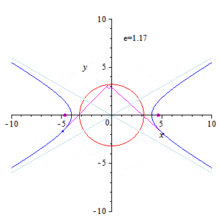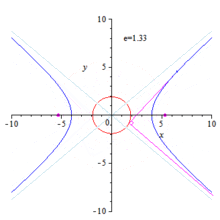
Orthoptics (red circles) of a circle, ellipses and hyperbolas

Orthoptic of an ellipse and hyperbola

Ellipse

Main article: Director circle

The ellipse with equation ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ can be represented by the unusual parametric representation^[1]

${\vec c}_{\pm }(m)=\left(-{\frac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}},{\frac {b^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\right),\,m\in \mathbb{R} ,$

where $m$ is the slope of the tangent at a point of the ellipse. ${\vec c}_{+}(m)$ describes the upper half and ${\vec c}_{-}(m)$ the lower half of the ellipse. The points $(\pm a,0)$ ) with tangents parallel to the y-axis are excluded. But this is no problem, because these tangents meet orthogonal the tangents parallel to the x-axis in the ellipse points $(0,\pm b)$ Hence the points $(\pm a,\pm b)$ are points of the desired orthoptic (circle $x^{2}+y^{2}=a^{2}+b^{2}$ ).

The tangent at point ${\vec c}_{\pm }(m)$ has the equation

y=mx\pm {\sqrt {m^{2}a^{2}+b^{2}}}.

If a tangent contains the point $(x_{0},y_{0})$ , off the ellipse, then the equation

y_{0}=mx_{0}\pm {\sqrt {m^{2}a^{2}+b^{2}}}

holds. Eliminatig the square root leads to

m^{2}-{\frac {2x_{0}y_{0}}{x_{0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=0,

which has two solutions $m_1,m_2$ corresponding to the two tangents passing point $(x_{0},y_{0})$ . The free term of a reduced quadratic equation is always the product of its solutions. Hence, if the tangents meet at point $(x_{0},y_{0})$ orthogonal, the following equations hold:

m_{1}m_{2}=-1={\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}

The last equation is equivalent to

x_{0}^{2}+y_{0}^{2}=a^{2}+b^{2}

This means:

The intersection points of orthogonal tangents are points of the circle $x^{2}+y^{2}=a^{2}+b^{2}$ .

Hyperbola

The ellipse case can be adopted nearly literally to the hyperbola case. The only changes to be made are: 1) replace $b^{2}$ by $-b^{2}$ and 2) restrict $m$ by $|m|>b/a$ . One gets:

The intersection points of orthogonal tangents are points of the circle $x^{2}+y^{2}=a^{2}-b^{2},\ a>b$ .

Orthoptic of an astroid

Orthoptic (purple) of an astroid

An astroid can be described by the parametric representation

{\vec c}(t)=(\cos ^{3}t,\sin ^{3}t),\;0\leq t<2\pi

From the condition ${\vec {\dot c}}(t)\cdot {\vec {\dot c}}(t+\alpha )=0$ one recognizes, at what distance $\alpha$ in parameter space an orthogonal tangent to ${\vec {\dot c}}(t)$ appears. It turns out, that the distance is independent of parameter $t$ , namely $\alpha =\pm {\tfrac {\pi }{2}}$ . The equations of the (orthogonal) tangents at the points ${\vec c}(t)$ and ${\vec c}(t+{\tfrac {\pi }{2}})$ are:

y=-\tan t(x-\cos ^{3}t)+\sin ^{3}t,\ y={\tfrac {1}{\tan t}}(x+\sin ^{3}t)+\cos ^{3}t

Their common point has coordinates:

x=\sin t\cos t(\sin t-\cos t)

y=\sin t\cos t(\sin t+\cos t)

This is at the same time a parametric representation of the orthoptic.

Elimination of parameter $t$ yields the implicit representation

2(x^{2}+y^{2})^{3}-(x^{2}-y^{2})^{2}=0.

Introducing the new parameter $\varphi =t-{\tfrac {5}{4}}\pi$ one gets

x={\tfrac {1}{{\sqrt {2}}}}\cos(2\varphi )\,\cos \varphi ,\ \ y={\tfrac {1}{{\sqrt {2}}}}\cos(2\varphi )\,\sin \varphi

. (proof uses Angle sum and difference identities.)

Herefrom we get the polar representation

r={\frac {1}{{\sqrt {2}}}}\cos(2\varphi ),\ 0\leq \varphi <2\pi

of the orthoptic. Hence

The orthoptic of an astroid is a quadrifolium.

Isoptic of a parabola, an ellipse and a hyperbola

Isoptics (purple) of a parabola for angles 80 and 100 degree

Isoptics (purple) of an ellipse for angles 80 and 100 degree

Isoptics (purple) of a hyperbola for angles 80 and 100 degree

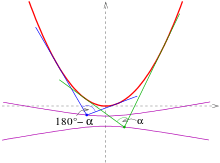
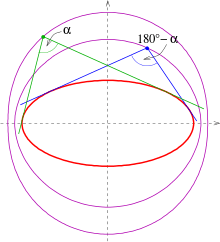
Below isotopics for an angle $\alpha \neq 90^{\circ }$ are listed. They are called $\alpha$ -isoptics. For the proofs: s. below.

Equations of the isoptics

parabola :

The $\alpha$ -isoptics of the parabola with equation $y=ax^{2}$ are the arms of the hyperbola

x^{2}-\tan ^{2}\alpha \left(y+{\frac {1}{4a}}\right)^{2}-{\frac {y}{a}}=0.

The arms of the hyperbola provide the isoptics for the two angles $\alpha ,180^{\circ }\!-\!\alpha$ (s. picture).

Ellipse:

The $\alpha$ -isoptics of the ellipse with equation ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ are the two parts of the curve of 4. degree

\tan ^{2}\alpha \;(x^{2}+y^{2}-a^{2}-b^{2})^{2}=4(a^{2}y^{2}+b^{2}x^{2}-a^{2}b^{2})

(s. picture).

Hyperbola:

The $\alpha$ -isoptics of the hyperbola with the equation ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$ are the two parts of the curve of 4. degree

\tan ^{2}\alpha \;(x^{2}+y^{2}-a^{2}+b^{2})^{2}=4(a^{2}y^{2}-b^{2}x^{2}+a^{2}b^{2}).

Proofs

Parabola:

A parabola $y=ax^{2}$ can be parametrized by the slope of its tangents $m=2ax$ :

{\vec c}(m)=\left({\frac {m}{2a}},{\frac {m^{2}}{4a}}\right),\,m\in \mathbb{R} .

The tangent with slope $m$ has the equation

y=mx-{\frac {m^{2}}{4a}}.

Point $(x_{0},y_{0})$ is on the tangent, if

y_{0}=mx_{0}-{\frac {m^{2}}{4a}}

holds. That means, the slopes $m_1,m_2$ of the two tangents containing $(x_{0},y_{0})$ fulfill the quadratic equation

m^{2}-4ax_{0}m+4ay_{0}=0.

If the tangents meet with angle $\alpha$ or $180^{\circ }-\alpha$ , the equation

\tan ^{2}\alpha =\left({\frac {m_{1}-m_{2}}{1+m_{1}m_{2}}}\right)^{2}

has to be fulfilled. Solving the quadratic equation for $m,$ inserting $m_1,m_2$ into the last equation, one gets

x_{0}^{2}-\tan ^{2}\alpha \left(y_{0}+{\frac {1}{4a}}\right)^{2}-{\frac {y_{0}}{a}}=0.

This is the equation of the hyperbola above. Its arms bear the two isoptics of the parabola for the two angles $\alpha$ and $180^{\circ }-\alpha$ .

Ellipse:

In case of an ellipse ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ one can adopt the idea for the orthoptic until the quadratic equation

m^{2}-{\frac {2x_{0}y_{0}}{x_{0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=0.

Now, as in case of a parabola, the quadratic equation has to be solved and the two solutions $m_1,m_2$ to be inserted into the equation $\tan ^{2}\alpha =\left({\tfrac {m_{1}-m_{2}}{1+m_{1}m_{2}}}\right)^{2}$ . Rearranging shows that the isoptics are parts of the curve of 4. degree:

\tan ^{2}\alpha \;(x_{0}^{2}+y_{0}^{2}-a^{2}-b^{2})^{2}=4(a^{2}y_{0}^{2}+b^{2}x_{0}^{2}-a^{2}b^{2}).

Hyperbola:

The solution for the case of a hyperbola can be adopted from the ellipse case by replacing $b^{2}$ by $-b^{2}$ (as in the case of the orthoptics, s. above).

Remark: For visualizing the isoptics see implicit curve.

External links

Wikimedia Commons has media related to Isoptics.

Notes

↑ P. K. Jain: Textbook of Analytical Geometry of two Dimensions. p. 214.

References

J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 58–59. ISBN 0-486-60288-5.
Boris Odehnal: Equioptic Curves of Conic Sections. Journal for Geometry and Graphics, Volume 14 (2010), No. 1, p. 29–43.
Hermann Schaal: Lineare Algebra und Analytische Geometrie. Band III, Vieweg, 1977, ISBN 3 528 03058 5, p. 220.
Jacob Steiner’s Vorlesungen über synthetische Geometrie. B. G. Teubner, Leipzig 1867 (bei Google Books), 2. Teil, p. 186.
Maurizio Ternullo: Two new sets of ellipse related concyclic points. Journal of Geometry 2009, 94, p. 159–173.

This article is issued from Wikipedia - version of the 9/21/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.