Giraud subcategory
In mathematics, Giraud subcategories form an important class of subcategories of Grothendieck categories. They are named after Jean Giraud.
Definition
Let 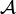 be a Grothendieck category. A full subcategory
be a Grothendieck category. A full subcategory 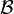 is called reflective, if the inclusion functor
is called reflective, if the inclusion functor 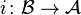 has a left adjoint. If this left adjoint of
has a left adjoint. If this left adjoint of 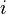 also preserves
kernels, then
also preserves
kernels, then 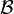 is called a Giraud subcategory.
is called a Giraud subcategory.
Properties
Let 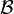 be Giraud in the Grothendieck category
be Giraud in the Grothendieck category 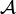 and
and 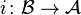 the inclusion functor.
the inclusion functor.
-
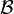 is again a Grothendieck category.
is again a Grothendieck category. - An object
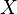 in
in 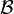 is injective if and only if
is injective if and only if 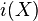 is injective in
is injective in 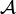 .
. - The left adjoint
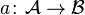 of
of 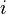 is exact.
is exact. - Let
 be a localizing subcategory of
be a localizing subcategory of 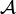 and
and 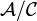 be the associated quotient category. The section functor
be the associated quotient category. The section functor 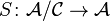 is fully faithful and induces an equivalence between
is fully faithful and induces an equivalence between 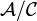 and the Giraud subcategory
and the Giraud subcategory 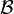 given by the
given by the 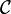 -closed objects in
-closed objects in 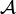 .
.
See also
References
- Bo Stenström; 1975; Rings of quotients. Springer.
This article is issued from Wikipedia - version of the 12/24/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.