Fundamental theorem on homomorphisms
In abstract algebra, the fundamental theorem on homomorphisms, also known as the fundamental homomorphism theorem, relates the structure of two objects between which a homomorphism is given, and of the kernel and image of the homomorphism.
The homomorphism theorem is used to prove the isomorphism theorems.
Group theoretic version
Given two groups G and H and a group homomorphism f : G→H, let K be a normal subgroup in G and φ the natural surjective homomorphism G→G/K (where G/K is a quotient group). If K is a subset of ker(f) then there exists a unique homomorphism h:G/K→H such that f = h φ.
In other words, the natural projection φ is universal among homomorphisms on G that map K to the identity element.
The situation is described by the following commutative diagram:
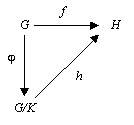
By setting K = ker(f) we immediately get the first isomorphism theorem.
Other versions
Similar theorems are valid for monoids, vector spaces, modules, and rings.
See also
References
- Beachy, John A. (1999), "Theorem 1.2.7 (The fundamental homomorphism theorem)", Introductory Lectures on Rings and Modules, London Mathematical Society Student Texts, 47, Cambridge University Press, p. 27, ISBN 9780521644075.
- Grove, Larry C. (2012), "Theorem 1.11 (The Fundamental Homomorphism Theorem)", Algebra, Dover Books on Mathematics, Courier Corporation, p. 11, ISBN 9780486142135.
- Jacobson, Nathan (2012), "Fundamental theorem on homomorphisms of Ω-algebras", Basic Algebra II, Dover Books on Mathematics (2nd ed.), Courier Corporation, p. 62, ISBN 9780486135212.
- Rose, John S. (1994), "3.24 Fundamental theorem on homomorphisms", A course on Group Theory [reprint of the 1978 original], Dover Publications, Inc., New York, pp. 44–45, ISBN 0-486-68194-7, MR 1298629.