Ergun equation

The Ergun equation, derived by the Turkish chemical engineer Sabri Ergun in 1952, expresses the friction factor in a packed column as a function of the modified Reynolds number.

Equation

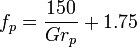
$f_p = \frac {150}{Gr_p} + 1.75$

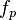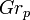where $f_p$ and $Gr_p$ are defined as

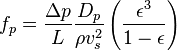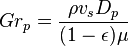
$f_p = \frac{\Delta p}{L} \frac{D_p}{\rho v_s^2} \left(\frac{\epsilon^3}{1-\epsilon}\right)$ and $Gr_p = \frac{\rho v_s D_p}{(1-\epsilon)\mu}$

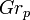where: $Gr_p$ is the modified Reynolds number,
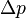$\Delta p$ is the pressure drop across the bed,
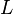$L$ is the length of the bed (not the column),
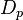$D_p$ is the equivalent spherical diameter of the packing,
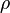$\rho$ is the density of fluid,
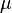$\mu$ is the dynamic viscosity of the fluid,
$v_s$ is the superficial velocity (i.e. the velocity that the fluid would have through the empty tube at the same volumetric flow rate), and
$\epsilon$ is the void fraction of the bed (bed porosity at any time).

Extension

The extension of the Ergun equation to fluidized beds is discussed by Akgiray and Saatçı (2001). To calculate the pressure drop in a given reactor, the following equation may be deduced

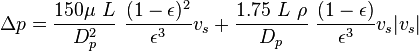
$\Delta p=\frac{150\mu ~L}{D_p^2} ~\frac{(1-\epsilon)^2}{\epsilon^3}v_s + \frac{1.75~L~\rho}{D_p}~ \frac{(1-\epsilon)}{\epsilon^3}v_s|v_s|$

This arrangement of the Ergun equation makes clear its close relationship to the simpler Kozeny-Carman equation which describes laminar flow of fluids across packed beds.

References

Ergun, Sabri. "Fluid flow through packed columns." Chem. Eng. Prog. 48 (1952).
Ö. Akgiray and A. M. Saatçı, Water Science and Technology: Water Supply, Vol:1, Issue:2, pp. 65–72, 2001.

This article is issued from Wikipedia - version of the 2/17/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Ergun equation

Equation

Extension

See also

References