Cyclic symmetry in three dimensions
 Involutional symmetry Cs, (*) [ ] = |
 Cyclic symmetry Cnv, (*nn) [n] = |
 Dihedral symmetry Dnh, (*n22) [n,2] = | |
| Polyhedral group, [n,3], (*n32) | |||
|---|---|---|---|
 Tetrahedral symmetry Td, (*332) [3,3] = |
 Octahedral symmetry Oh, (*432) [4,3] = |
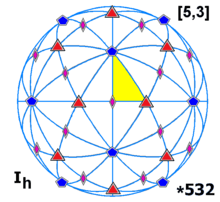 Icosahedral symmetry Ih, (*532) [5,3] = | |
In three dimensional geometry, there are four infinite series of point groups in three dimensions (n≥1) with n-fold rotational or reflectional symmetry about one axis (by an angle of 360°/n) does not change the object.
They are the finite symmetry groups on a cone. For n = ∞ they correspond to four frieze groups. Schönflies notation is used. The terms horizontal (h) and vertical (v) imply the existence and direction of reflections with respect to a vertical axis of symmetry. Also shown are Coxeter notation in brackets, and, in parentheses, orbifold notation.
Types
- Chiral
- Cn, [n]+, (nn) of order n - n-fold rotational symmetry - acro-n-gonal group (abstract group Zn); for n=1: no symmetry (trivial group)
- Achiral

- Cnh, [n+,2], (n*) of order 2n - prismatic symmetry or ortho-n-gonal group (abstract group Zn × Dih1); for n=1 this is denoted by Cs (1*) and called reflection symmetry, also bilateral symmetry. It has reflection symmetry with respect to a plane perpendicular to the n-fold rotation axis.
- Cnv, [n], (*nn) of order 2n - pyramidal symmetry or full acro-n-gonal group (abstract group Dihn); in biology C2v is called biradial symmetry. For n=1 we have again Cs (1*). It has vertical mirror planes. This is the symmetry group for a regular n-sided pyramid.
- S2n, [2+,2n+], (n×) of order 2n - gyro-n-gonal group (not to be confused with symmetric groups, for which the same notation is used; abstract group Z2n); It has a 2n-fold rotoreflection axis, also called 2n-fold improper rotation axis, i.e., the symmetry group contains a combination of a reflection in the horizontal plane and a rotation by an angle 180°/n. Thus, like Dnd, it contains a number of improper rotations without containing the corresponding rotations.
- for n=1 we have S2 (1×), also denoted by Ci; this is inversion symmetry.
C2h, [2,2+] (2*) and C2v, [2], (*22) of order 4 are two of the three 3D symmetry group types with the Klein four-group as abstract group. C2v applies e.g. for a rectangular tile with its top side different from its bottom side.
Frieze groups
In the limit these four groups represent Euclidean plane frieze groups as C∞, C∞h, C∞v, and S∞. Rotations become translations in the limit. Portions of the infinite plane can also be cut and connected into an infinite cylinder.
| Notations | Examples | ||||
|---|---|---|---|---|---|
| IUC | Orbifold | Coxeter | Schönflies* | Euclidean plane | Cylindrical (n=6) |
| p1 | ∞∞ | [∞]+ | C∞ |  | |
| p1m1 | *∞∞ | [∞] | C∞v |  | |
| p11m | ∞* | [∞+,2] | C∞h |  | |
| p11g | ∞× | [∞+,2+] | S∞ |  | |
Examples
| S2/Ci (1x): | C4v (*44): | C5v (*55): | |
|---|---|---|---|
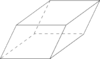 Parallelepiped |
 Square pyramid |
 Elongated square pyramid |
 Pentagonal pyramid |
See also
References
- Sands, Donald E. (1993). "Crystal Systems and Geometry". Introduction to Crystallography. Mineola, New York: Dover Publications, Inc. p. 165. ISBN 0-486-67839-3.
- On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN 978-1-56881-134-5
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- N.W. Johnson: Geometries and Transformations, (2015) Chapter 11: Finite symmetry groups