Blancmange curve

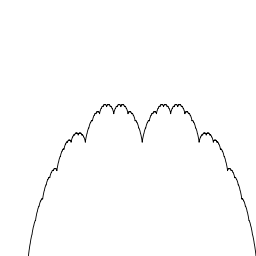
In mathematics, the blancmange curve is a fractal curve constructible by midpoint subdivision. It is also known as the Takagi curve, after Teiji Takagi who described it in 1901, or as the Takagi–Landsberg curve, a generalization of the curve named after Takagi and Georg Landsberg. The name blancmange comes from its resemblance to a pudding of the same name. It is a special case of the more general de Rham curve.

Definition

The blancmange function is defined on the unit interval by

{\rm blanc}(x) = \sum_{n=0}^\infty {s(2^{n}x)\over 2^n},

where $s(x)$ is the triangle wave, defined by $s(x)=\min_{n\in{\bold Z}}|x-n|$ , that is, $s(x)$ is the distance from x to the nearest integer.

The Takagi–Landsberg curve is a slight generalization, given by

T_w(x) = \sum_{n=0}^\infty w^n s(2^{n}x)

for a parameter w; thus the blancmange curve is the case $w=1/2$ . The value $H=-\log_2 w$ is known as the Hurst parameter.

The function can be extended to all of the real line: applying the definition given above shows that the function repeats on each unit interval.

Graphical construction

The blancmange curve can be visually built up out of triangle wave functions if the infinite sum is approximated by finite sums of the first few terms. In the illustration below, progressively finer triangle functions (shown in red) are added to the curve at each stage.


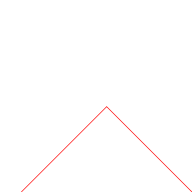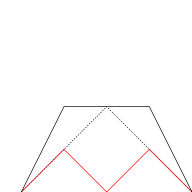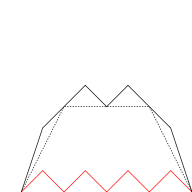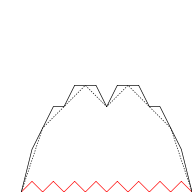n = 0	n ≤ 1	n ≤ 2	n ≤ 3

Properties

Convergence and continuity

The infinite sum defining $T_w(x)$ converges absolutely for all x: since $0\le s(x) \le 1/2$ for all $x\in \mathbb{R}$ , we have:

\sum_{n=0}^\infty |w^n s(2^n x)| \le 1/2 \sum_{n=0}^\infty |w|^n = \frac{1}{2} \cdot \frac{1}{1-|w|}

|w|<1

Therefore, the Takagi curve of parameter w is defined on the unit interval (or $\mathbb {R}$ ) if $|w|<1$ .

The Takagi function of parameter w is continuous. Indeed, the functions $T_{w,n}$ defined by the partial sums $T_{w,n}(x) = \sum_{k=0}^n w^k s(2^k x)$ are continuous and converge uniformly toward $T_w$ , since:

\left|T_w(x) - T_{w,n}(x)\right| = \left|\sum_{k=n+1}^\infty w^k s(2^k x)\right| = \left|w^{n+1} \sum_{k=0}^\infty w^k s(2^{k+n+1} x)\right| \le \frac{|w|^{n+1}}{2} \cdot \frac{1}{1-|w|}

for all x when

|w| < 1

This value can be made as small as we want by selecting a big enough value of n. Therefore, by the uniform limit theorem, $T_w$ is continuous if |w|<1.

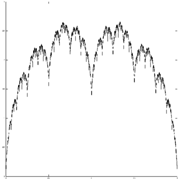
parameter w=2/3
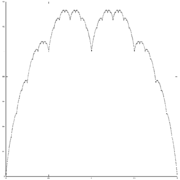
parameter w=1/2
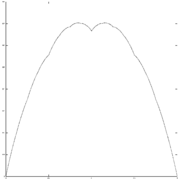
parameter w=1/3
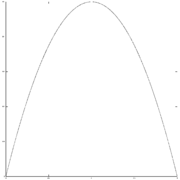
parameter w=1/4
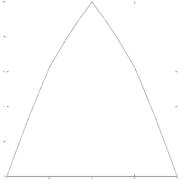
parameter w=1/8

The special case of the parabola

For $w=1/4$ , one obtains the parabola: the construction of the parabola by midpoint subdivision was described by Archimedes.

Differentiability

The Takagi curve is a fractal for parameters $\scriptstyle w \ne 1/4$ , as it is nowhere differentiable in the classic definition of delta-epsilon differentiability on the real number line (that is, w.r.t. the natural topology on the reals). However, by instead representing a real number as a 2-adic expansion of binary bits, one may temporarily adopt the product topology of the Cantor set, and immediately give meaning of the differential as a formal sum. That is, by noting that the derivative of a triangle wave is a square wave (equivalently, the repeated Haar mother wavelet):

\frac{d}{dx} s(x) = - \mbox{sgn}\left(x-\frac{1}{2}\right) = \begin{cases} +1 \mbox{ for } 0 < x < \frac{1}{2} \\ -1 \mbox{ for } \frac{1}{2} < x < 1 \end{cases}

one may immediately write the formal sum

\frac{d}{dx} T_w(x) = \sum_{n=0}^\infty (2w)^n \, \mbox{sgn} \left(s \left(2^n x - \frac{1}{4} \right)-\frac{1}{2} \right)

This sum is manifestly convergent for $w<1/2$ , although it is ill-defined at all dyadic rationals. It is the temporary adoption of the product topology that allows this formal manipulation to be given a practical meaning. Thus, it is more accurate to say that the Takagi curve is not differentiable on the dyadic rationals; it is "well-behaved" elsewhere (on the irrationals, and the non-dyadic rationals). The derivative is discontinuous at all dyadic rationals.

Equivalently, one may apply the discrete wavelet transform to obtain a representation in terms of Haar wavelets $\psi_{n,k}(x)$ ; the wavelet coefficients take a particularly simple form:

\frac{d}{dx} T_w(x) = \sum_{n=0}^\infty 2^{n/2} w^n \, \psi_{n,0} (x)

Fourier series expansion

The Takagi-Landsberg function admits an absolutely convergent Fourier series expansion:

T_w(x) =\sum_{m=0}^\infty a_m\cos(2\pi m x)

with $\scriptstyle a_0=1/4(1-w)$ and, for $\scriptstyle m\ge 1$

a_m:=-\frac{2}{\pi^2m^2}(4w)^{\nu(m)}\, ,

where $\scriptstyle 2^{\nu(m)}$ is the maximum power of $2$ that divides $m$ . Indeed, the above triangle wave $s(x)$ has an absolutely convergent Fourier series expansion

s(x)=\frac{1}{4}-\frac{2}{\pi^2}\sum_{k=0}^\infty\frac{1}{(2k+1)^2}\cos\big(2\pi (2k+1)x\big).

By absolute convergence, one can reorder the corresponding double series for $T_w(x)$ :

T_w(x):=\sum_{n=0}^\infty w^n s(2^nx)= \frac{1}{4}\sum_{n=0}^\infty w^n -\frac{2}{\pi^2}\sum_{n=0}^\infty\sum_{k=0}^\infty \frac{w^n}{ (2k+1)^2}\cos\big(2\pi 2^n(2k+1)x\big)\, :

putting $\scriptstyle m:=2^n(2k+1)$ yields the above Fourier series for $\scriptstyle T_w(x)$ .

Recursive definition

The periodic version of the Takagi curve can also be defined recursively by:

T_w(x) = s(x) + w T_w(2x)

The version restricted to the unit interval can also be defined recursively by:

T_w(x) = \begin{cases} x + w T_w(2x) & \text{if }0\leq x\leq 1/2 \\ (1-x) + w T_w(2x-1) & \text{if }1/2 < x\leq 1. \end{cases}

Proof:

\begin{align} T_w(x) &= \sum_{n=0}^\infty w^n s(2^{n}x)\\ &= s(x) + \sum_{n=1}^\infty w^n s(2^{n}x)\\ &= s(x) + w\sum_{n=0}^\infty w^n s(2^{n+1}x)\\ &= s(x) + wT_w(2x) \end{align}

Observe that this definition has the form of a discrete wavelet transform; thus the coefficients of the wavelet transform take a particularly simple form.

Self similarity

The above recursive definition allows the monoid of self-symmetries of the curve to be given. This monoid is given by two generators, g and r, which act on the curve (restricted to the unit interval) as

[g \cdot T_w](x) = T_w\left(\frac{x}{2}\right) = \frac{x}{2} + w T_w(x)

and

[r \cdot T_w](x) = T_w(1-x) = T_w(x)

A general element of the monoid then has the form $\gamma=g^{a_1} r g^{a_2} r \cdots r g^{a_n}$ for some integers $a_1, a_2, \cdots, a_n$ This acts on the curve as a linear function: $\gamma \cdot T_w = a + bx + cT_w$ for some constants a, b and c. Because the action is linear, it can be described in terms of a vector space, with the vector space basis:

1 \mapsto e_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}

x \mapsto e_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}

T_w \mapsto e_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}

In this representation, the action of g and r are given by

g=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} \\ 0 & 0 & w \end{bmatrix}

and

r=\begin{bmatrix} 1 & 1 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix}

That is, the action of a general element $\gamma$ maps the blancmange curve on the unit interval [0,1] to a sub-interval $[m/2^p, n/2^p]$ for some integers m, n, p. The mapping is given exactly by $[\gamma \cdot T_w](x) = a + bx + cT_w(x)$ where the values of a, b and c can be obtained directly by multiplying out the above matrices. That is:

\gamma=\begin{bmatrix} 1 & \frac{m}{2^p} & a \\ 0 & \frac{n-m}{2^p} & b \\ 0 & 0 & c \end{bmatrix}

Note that $p=a_1+a_2+\cdots +a_n$ is immediate.

The monoid generated by g and r is sometimes called the dyadic monoid; it is a sub-monoid of the modular group. When discussing the modular group, the more common notation for g and r is T and S, but that notation conflicts with the symbols used here.

The above three-dimensional representation is just one of many representations it can have; it shows that the blancmange curve is one possible realization of the action. That is, there are representations for any dimension, not just 3; some of these give the de Rham curves.

Integrating the Blancmange curve

Given that the integral of ${\rm blanc}(x)$ from 0 to 1 is 1/2, the identity ${\rm blanc}(x)= {\rm blanc}(2x)/2+s(x)$ allows the integral over any interval to be computed by the following relation. The computation is recursive with computing time on the order of log of the accuracy required. Defining

I(x) = \int_0^x{\rm blanc}(x)\,dx

one has that

I(x) =\begin{cases} I(2x)/4+x^2/2 & \text{if } 0 \leq x \leq 1/2 \\ 1/2-I(1-x) & \text{if } 1/2 \le x \le 1 \\ n/2+I(x-n) & \text{if } n \le x \le (n+1) \\ \end{cases}

The definite integral is given by:

\int_a^b{\rm blanc}(x)\,dx = I(b) - I(a).

A more general expression can be obtained by defining

S(x)=\int _{0}^{x}s(y)dy={\begin{cases}x^{2}/2&{\mbox{ for }}0\leq x\leq {\frac {1}{2}}\\-x^{2}/2+x-1/4&{\mbox{ for }}{\frac {1}{2}}\leq x\leq 1\\n/4+S(x-n)&{\mbox{ for }}(n\leq x\leq n+1)\end{cases}}

which, combined with the series representation, gives

I_w(x)= \int_0^x T_w(x) dx = \sum_{n=0}^\infty (w/2)^n S(2^n x)

Note that

I_w(1)=\frac{1}{4(1-w)}

This integral is also self-similar on the unit interval, under an action of the same dyadic monoid as described above. Here, the representation is 4-dimensional, having the basis $\{1, x, x^2, I(x)\}$ . Re-writing the above to make the action of g more clear: on the unit interval, one has

[g\cdot I_w](x) = I_w\left(\frac{x}{2}\right) = \frac{x^2}{8} + \frac{w}{2}I_w(x)

From this, one can then immediately read off the generators of the four-dimensional representation:

g=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \frac{1}{2} & 0 & 0 \\ 0 & 0 & \frac{1}{4} & \frac{1}{8} \\ 0 & 0 & 0 & \frac{w}{2} \end{bmatrix}

and

r=\begin{bmatrix} 1 & 1 & 1 & \frac{1}{4(1-w)} \\ 0 & -1 & -2 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix}

Repeated integrals transform under a 5,6,... dimensional representation.

Relation to simplicial complexes

Let

N=\binom{n_t}{t}+\binom{n_{t-1}}{t-1}+\ldots+\binom{n_j}{j},\quad n_t > n_{t-1} > \ldots > n_j \geq j\geq 1.

Define the Kruskal–Katona function

\kappa_t(N)={n_t \choose t+1} + {n_{t-1} \choose t} + \dots + {n_j \choose j+1}.

The Kruskal–Katona theorem states that this is the minimum number of (t − 1)-simplexes that are faces of a set of N t-simplexes.

As t and N approach infinity, $\kappa_t(N)-N$ (suitably normalized) approaches the blancmange curve.

References

Weisstein, Eric W. "Blancmange Function". MathWorld.

Takagi, Teiji (1901), "A Simple Example of the Continuous Function without Derivative", Proc. Phys. Math. Japan, 1: 176–177, doi:10.11429/subutsuhokoku1901.1.F176
Benoit Mandelbrot, "Fractal Landscapes without creases and with rivers", appearing in The Science of Fractal Images, ed. Heinz-Otto Peitgen, Dietmar Saupe; Springer-Verlag (1988) pp 243–260.
Linas Vepstas, Symmetries of Period-Doubling Maps, (2004)
Donald Knuth, The Art of Computer Programming, volume 4a. Combinatorial algorithms, part 1. ISBN 0-201-03804-8. See pages 372-375.

External links

This article is issued from Wikipedia - version of the 2/4/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.