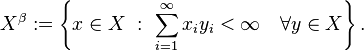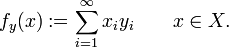Beta-dual space
In functional analysis and related areas of mathematics, the beta-dual or β-dual is a certain linear subspace of the algebraic dual of a sequence space.
Definition
Given a sequence space X the β-dual of X is defined as
If X is an FK-space then each y in Xβ defines a continuous linear form on X
Examples
Properties
The beta-dual of an FK-space E is a linear subspace of the continuous dual of E. If E is an FK-AK space then the beta dual is linear isomorphic to the continuous dual.
This article is issued from Wikipedia - version of the 3/12/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.